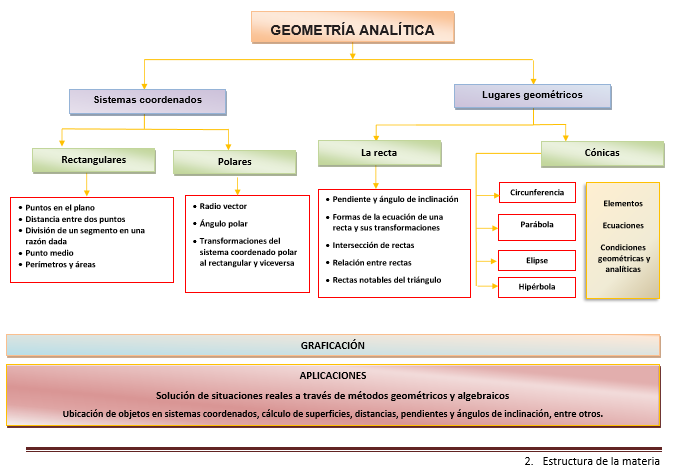
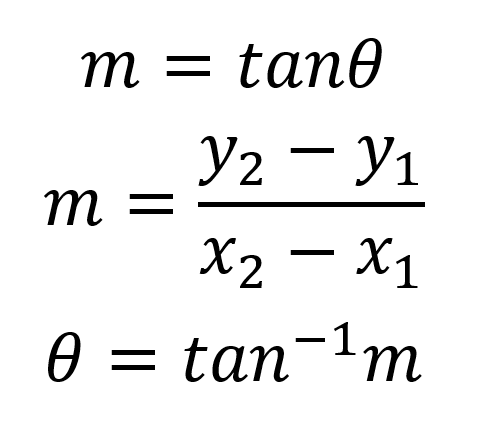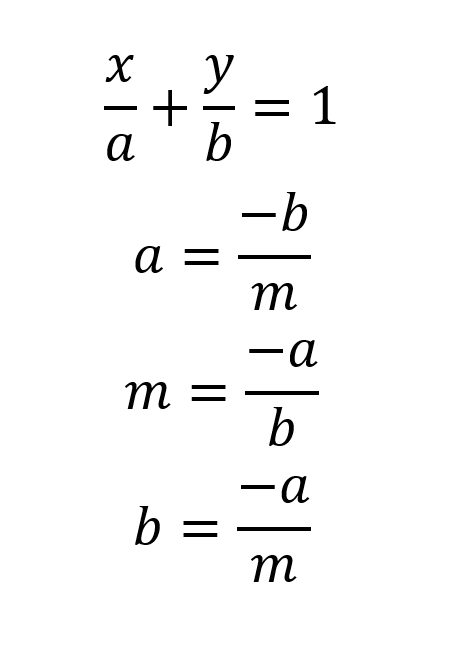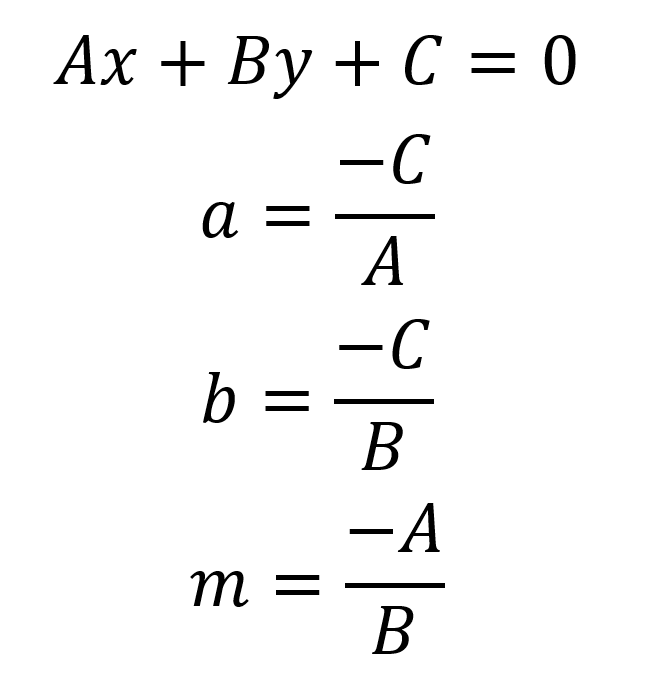Geometría analítica
La Geometría Analítica: es la rama de las matemáticas en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante expresiones algebraicas y usando un conjunto de ejes y coordenadas. Cualquier punto del plano se puede localizar con respecto a un par de ejes perpendiculares dando las distancias del punto a cada uno de los ejes.
La historia de las Matemáticas considera a René Descartes el fundador de la Geometría Analítica, la cual fusiona el Álgebra con la Geometría referidas a un sistema de coordenadas (plano cartesiano), por métodos algebraicos.
Plano cartesiano
El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o eje (y); el punto donde se cortan recibe el nombre de origen.

Distancia entre dos puntos
Un segmento de recta es utilizado para determinar la distancia entre dos puntos, es decir, la longitud del segmento que une estos dos puntos. Cuando nos proporcionan dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa. Para calcular la distancia aplicamos el teorema de Pitágoras del cual obtenemos la siguiente fórmula:

U2 T1 Actividad 1 - Distancia entre dos puntos

En tu cuaderno, resuelve los siguientes ejercicios encontrando la distancia entre dos puntos y ubicándolos en el plano cartesiano.
- C(2,6), C(0,3)
- E(-4,5), F(2,2)
- A(0,-2), B(5,-1)
- U(5,-3), V(-5,-3)
- M(-6,3), N(2,-3)
- O(6,1), P(-4,-2)
- R(4,4), S(4,-1)
- X(-3,-1), Y(7,-5)
- Comprueba que los siguientes vértices A(-3,1), B(-4,-3) y C(5,-4), son los vértices de un triángulo rectángulo y calcula las distancias entre cada uno de sus lados
- Comprueba que los siguientes vértices A(-5,0), B(0,5) y C(5,0), son los vértices de un triángulo rectángulo y calcula las distancias entre cada uno de sus lados
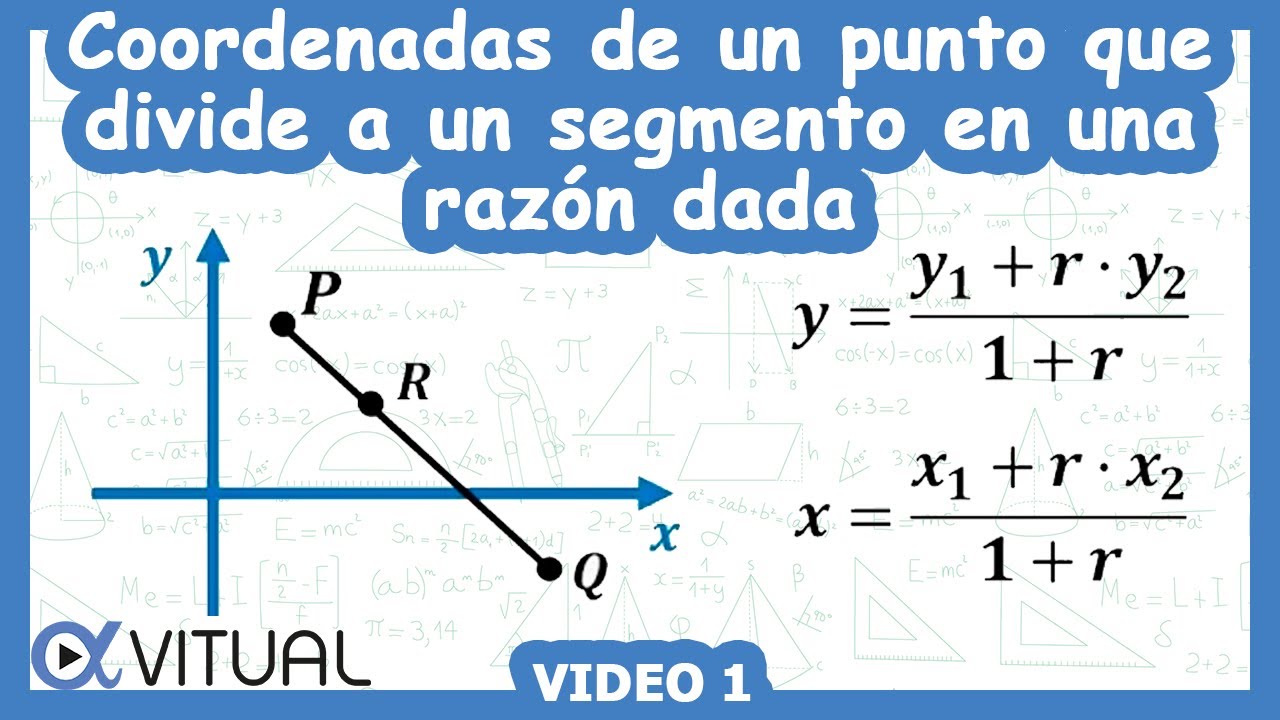
División de un segmento en una razón dada
Consideramos como el proceso de “Dividir un segmento en una razón dada” aquel el cual consiste en determinar un punto (P) el cual se encuentra dentro de un segmento dado, entre dos puntos (P1) y (P2), de tal manera que el segmento (P1P) dividido entre el segmento (PP2) da como resultado la razón.
U2 T1 Actividad 2 - División de un segmento en una razón dada

En tu cuaderno, resuelve los siguientes ejercicios encontrando la división de un segmento en una razón dada y ubica los puntos en el plano cartesiano.
- A(-2,-4), B(1,6), r=2
- M(8,7), N(-2,-1), r=4
- Q(-3,7), R(2,3), r=3
- P(-7,-7), C(8,10), r=5
- A(1,1), B(5,6), r=2/3
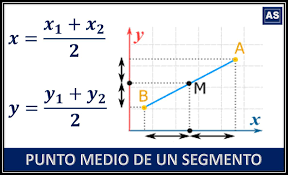
Punto medio de un segmento
El punto medio, es el punto que se encuentra a la misma distancia de otros dos puntos cualquiera o extremos de un segmento. Si es un segmento, el punto medio es el que lo divide en dos partes iguales.
U2 T1 Actividad 3 - Punto medio de un segmento

En tu cuaderno, resuelve los siguientes ejercicios encontrando el punto medio de un segmento localizándolos en el plano cartesiano.
- A(8,4), B(-2,0)
- A(4,5), B(-1,1)
- A(-4,3), B(5,-2)
- R(-6,4), S(3,1)
- C(0,1), B(3,-1)
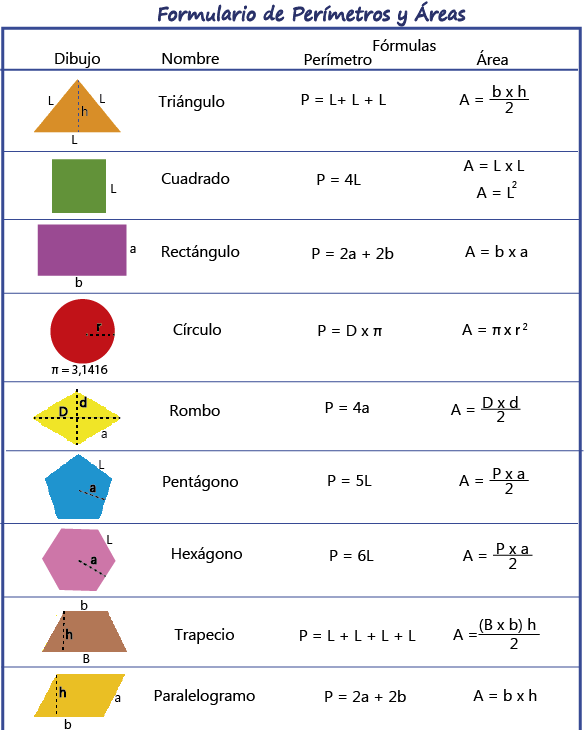
Perímetros y áreas en plano cartesiano

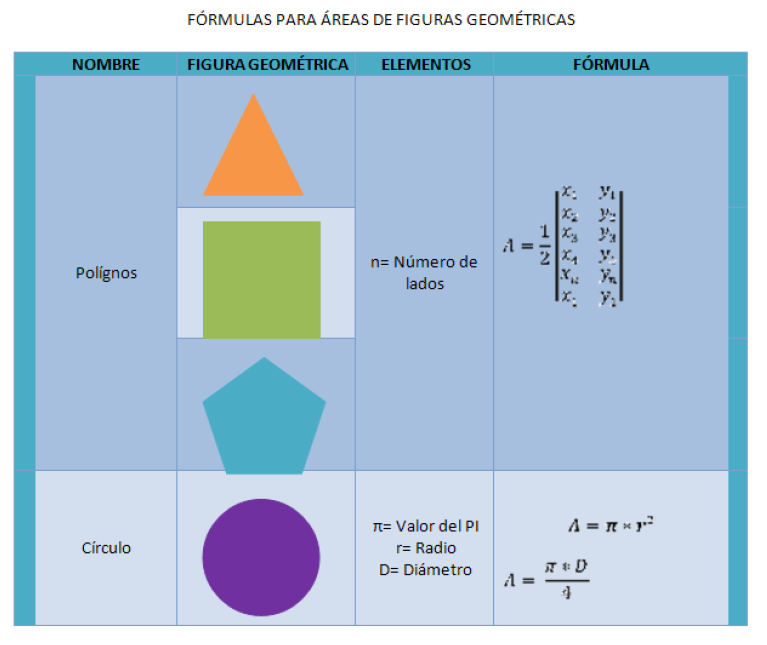

U2 T1 Actividad 4 - Perímetros y áreas en plano cartesiano

En tu cuaderno, resuelve los siguientes ejercicios encontrando el área y perímetro de las siguientes coordenadas. A(-3,1), B(4,1), C(1,6).
U2 T1 Actividad 5 - Perímetros y áreas en plano cartesiano

En tu cuaderno, resuelve los siguientes ejercicios ubicando los puntos en el plano cartesiano y encontrando el área y perímetro de las siguientes coordenadas.
- A(-3,-5), B(3,-5), C(1,5)
- A(-3,-4), B(3,-6), C(2,6)
- A(-5,1), B(-5,6), C(5,6), D(5,1)
- A(-5,0), B(-5,6), C(-3,7), D(5,6), E(5,0)
Ecuaciones de la recta
- Punto pendiente
- Dos puntos
- Pendiente y ordenada al origen (ecuación común)
- Abscisa y ordenada al origen (ecuación simétrica)
- Forma general
- Ecuación normal
Fórmulas para calcular la pendiente
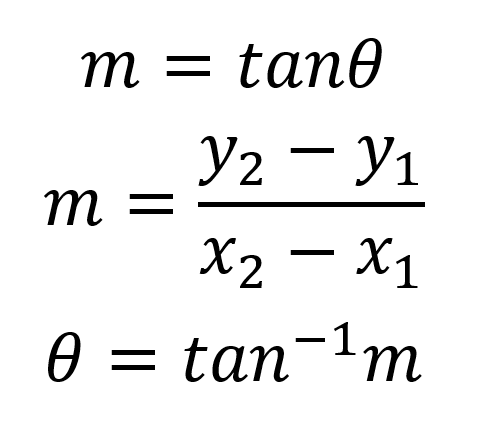
Punto pendiente
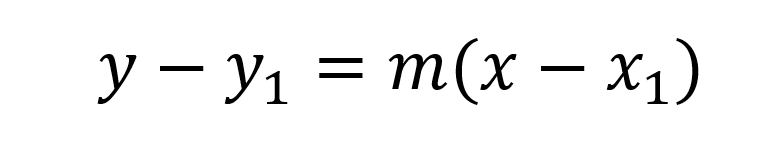
Ecuación de la recta "pendiente y ordenada al origen" ecuación común
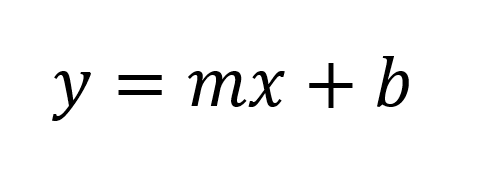
Ecuación de la recta con abscisa y ordenada al origen (ecuación simétrica)
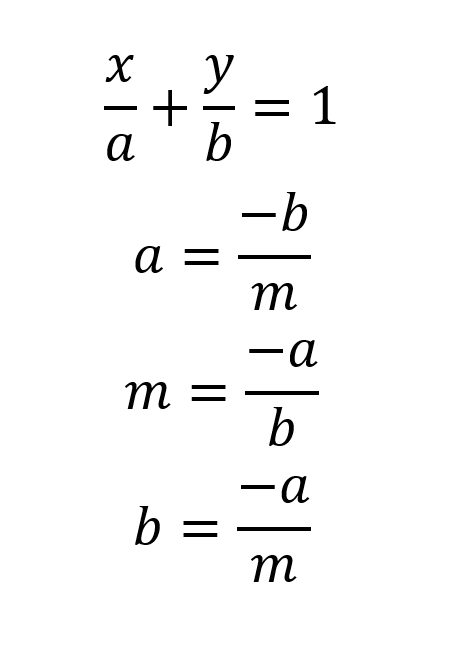
Ecuación general
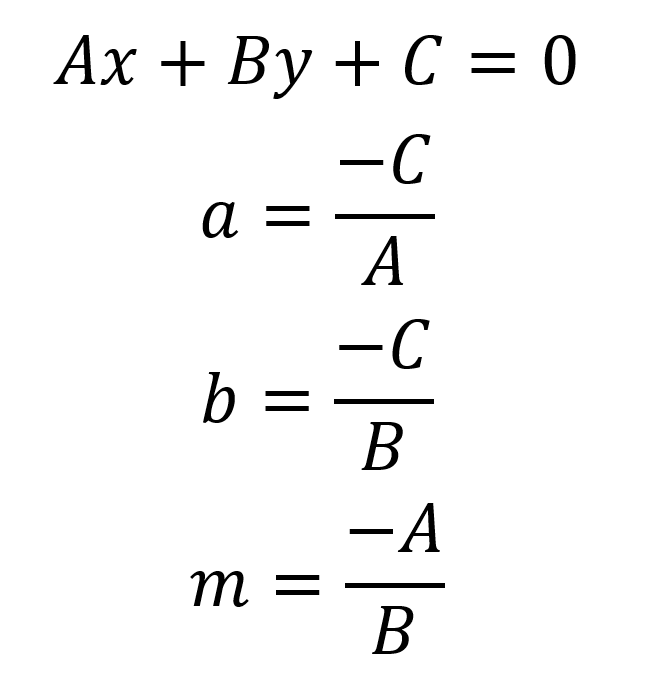




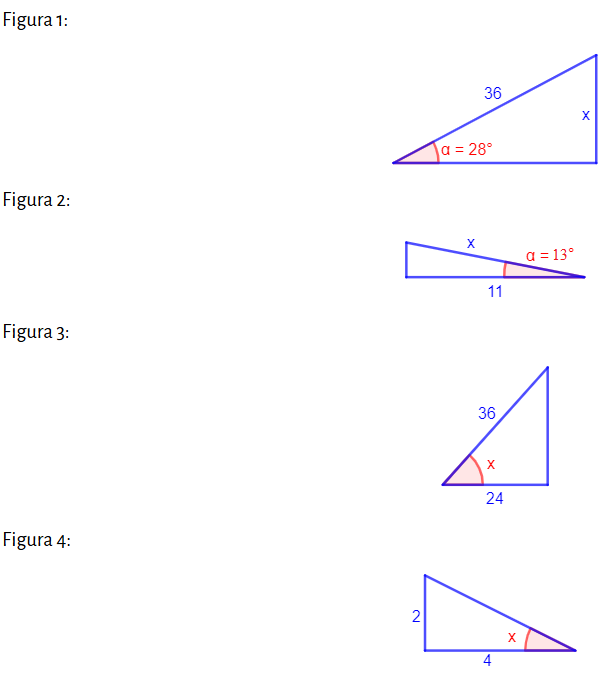
 Funciones trigonométricas
Funciones trigonométricas