Cálculo Diferencial

Aunque su origen puede ser considerado con la civilización Babilónica a partir del periodo del 2000 al 500 a.C., su terminología surge a principios del siglo XVII donde un matemático alemán llamado Johannes Kepler estudiaba los análisis astronómicos realizados por Tycho Brahe, en donde pudo observar que los planetas se mueven alrededor del sol en órbitas elípticas, sin embargo, no sabía el por qué. Ya pasado el tiempo, cincuenta años después, un matemático y físico inglés llamado Isaac Newton, supó la respuesta.

Todas las cuestiones relacionadas con el análisis del movimiento y la manera en que las magnitudes cambian con respecto al tiempo o a otra magnitud, necesitan de operaciones que van más allá de las algebraicas, y que midan la forma en la que van variando las magnitudes relacionadas, es aquí donde surge el cálculo, donde proporcionando herramientas como la diferenciación e integración, se puede describir como contrarias entre sí, ya que lo que hace la diferenciación, lo deshace la integración.

En el siguiente enlace viene la información completa acerca de la historia del cálculo:

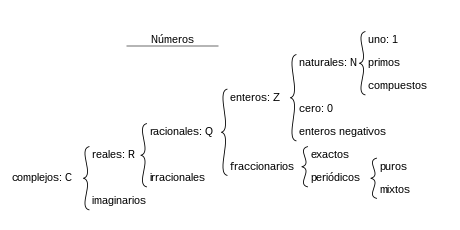
En el siguiente recurso viene la información sobre la clasificación de los números (naturales o positivos, enteros, racionales e irracionales):

Indicaciones: Menciona cinco ejemplos de cada uno de los siguientes tipos de números:

1. Naturales o positivos
2. Enteros
3. Racionales
4. Irracionales

Los números reales se pueden acomodar geométricamente como puntos en una recta real.

Indicaciones: Acomoda los siguientes puntos en la recta real.

1. Math.Sqrt(2)
2. Math.PI
3. -2
4. -3/4
5. -1
6. 0
7. 2
8. 1/3
9. 3
10. 4
11. 1

Son los subconjuntos de la recta real en la cual se representan a partir de dos números y deben ser reales. Pueden ser de intervalo abierto, cerrado o semiabierto.

Indicaciones: Resuelve las siguientes expresiones y representalas como un intervalo:

1. 5 < x < 10
2. -10 <= x <= 10
3. 2x -1 > x + 3
4. -x/3 >= 2x -1
5. 10x - 6 < x -5

El valor absoluto o módulo de un número x, se representa |x|, si x es >= 0 y -x es < 0.

Si |x - y| = { x - y, si x >= y }

Si |x - y| = { y - x, si x < y }

Nota: siempre se pone el valor menor de lado izquierdo.

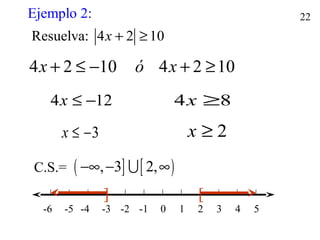
Indicaciones: Resuelve las siguientes expresiones:

1. |2x + 3| >= 5
2. 5 + |x + 1| = 10
3. |x - 10| = 5
4. |2x - 2| < 4
5. -x/3 >= 2x -1

El área de un círculo depende de su radio. La temperatura de ebullición del agua depende de la altitud respecto al nivel del mar. El interés de una inversión depende del tiempo que se mantenga aquélla. Siempre que una cantidad dependa de otra, se dice que la primera es función de la segunda. Por ejemplo, el área A de un círculo depende de su radio r de acuerdo con la fórmula:

A = PI*r^2

El conjutno de todos los posibles valores del radio se denomina dominio de la función. El conjunto de todos los posibles valores del área es el rango de la función. Para indicar que y es una función de x se escribe:

y = f(x)

En esta notación, debida al matemático del siglo XIX Leonhard Euler, la función se representa mediante el símbolo f. La variable x, denominada variable independiente, representa un valor de entrada del dominio de f. La variable y, denominada variable dependiente, representa el correspondiente valor de salida f(x) en el intervalo de f.

Una función f de un conjunto D en un conjunto S es una regla que asigna un único elemento f(x) de S a cada uno de los elementos x de D.

1. Mediante una fórmula como y = x^2, que utiliza una variable dependiente y para indicar el valor de la función.
2. Mediante una fórmula como f(x) = x^2, que define un símbolo de función f para indicar la función.
3. Mediante una regla de transofmración como x -> x^2 (léase < < x se transforma en x^2 > > )

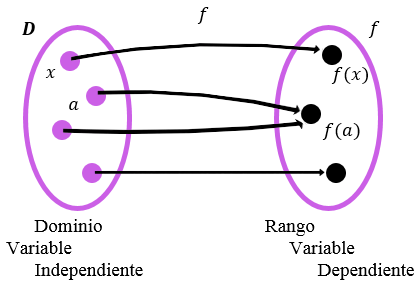
Supongamos que -x pertenece al dominio de una función cuando x pertenece a dicho dominio. Se dice que f es una función par si:

f(-x) = f(x) para todo x en el dominio de f

Se dice que f es una función impar si:

f(-x) = -f(x) para todo x en el dominio de f

Da clic en la siguiente imagen para acceder al documento PDF sobre los tipos de gráficas de funciones:

Indicaciones: Resuelve los siguientes ejercicios:

Da clic en la siguiente imagen para conocer acerca de las funciones:

Para poder hablar con sentido sobre tasas de cambio, rectas tangentes y áreas encerradas por curvas, es necesario investigar previamente el procedimiento de obtención de límites. De hecho, el concepto de límite es la piedra angular sobre la que descansa el desarrollo del cálculo. Antes de intentar una definición de límite.

Indicaciones: Resuelve los siguientes ejercicios:

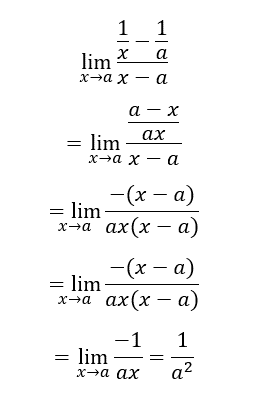
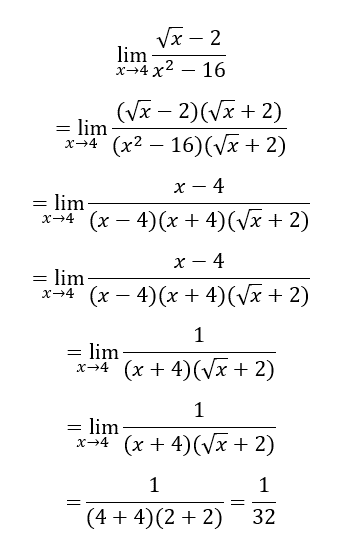
Indicaciones: Utilizando el enlace anterior, en equipos, seleccionen tres tipos de límites y expliquen el procedimiento para resolverlos. Pueden apoyarse de una presentación o bien con los marcadores. Los ejemplos deben ser de distancia diez entre cada uno.

Indicaciones: En hojas de máquina, resuelve los siguientes ejercicios. Agrega una portada. Después, sube esta evaluación en formato PDF a Moodle.

En el siguiente enlace conocerás la historia del cálculo diferencial:

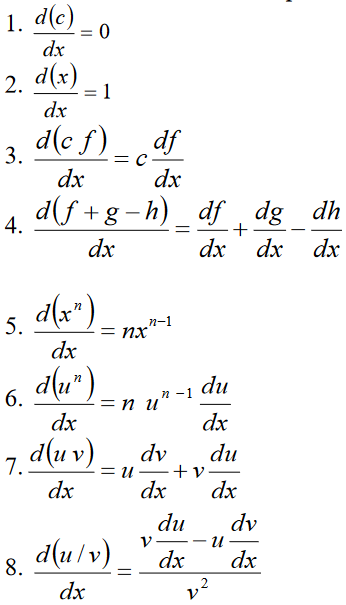
Toda la siguiente información es tomada del documento cálculo diferencial, del profesor Eduardo Becerril Espinosa:

Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

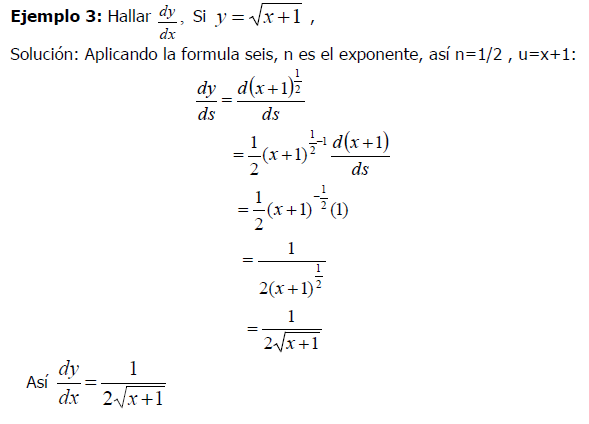
Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

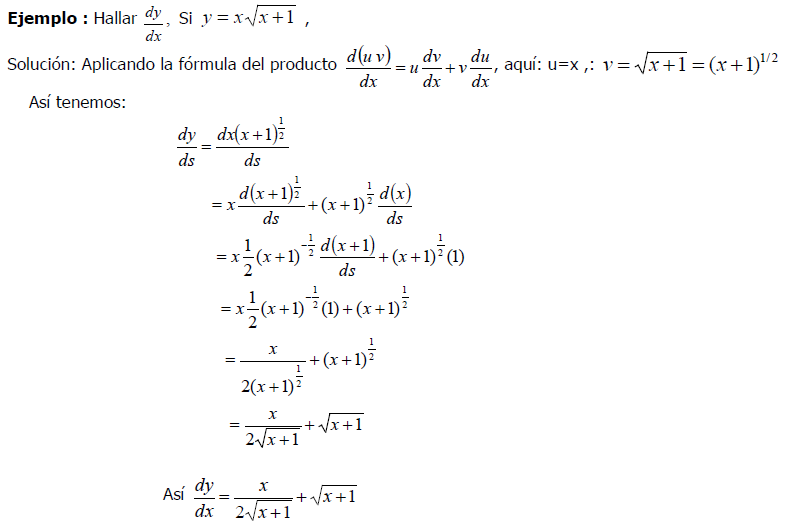
Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

Indicaciones: En tu cuaderno resuelve los siguientes ejercicios:

Indicaciones: En hojas de máquina, resuelve los siguientes ejercicios. Agrega una portada. Después, sube esta evaluación en formato PDF a Moodle.

Da clic en la siguiente imagen para acceder al recurso sobre máximos y mínimos:

Da clic en la siguiente imagen para acceder al video sobre la metodología de la optimización:

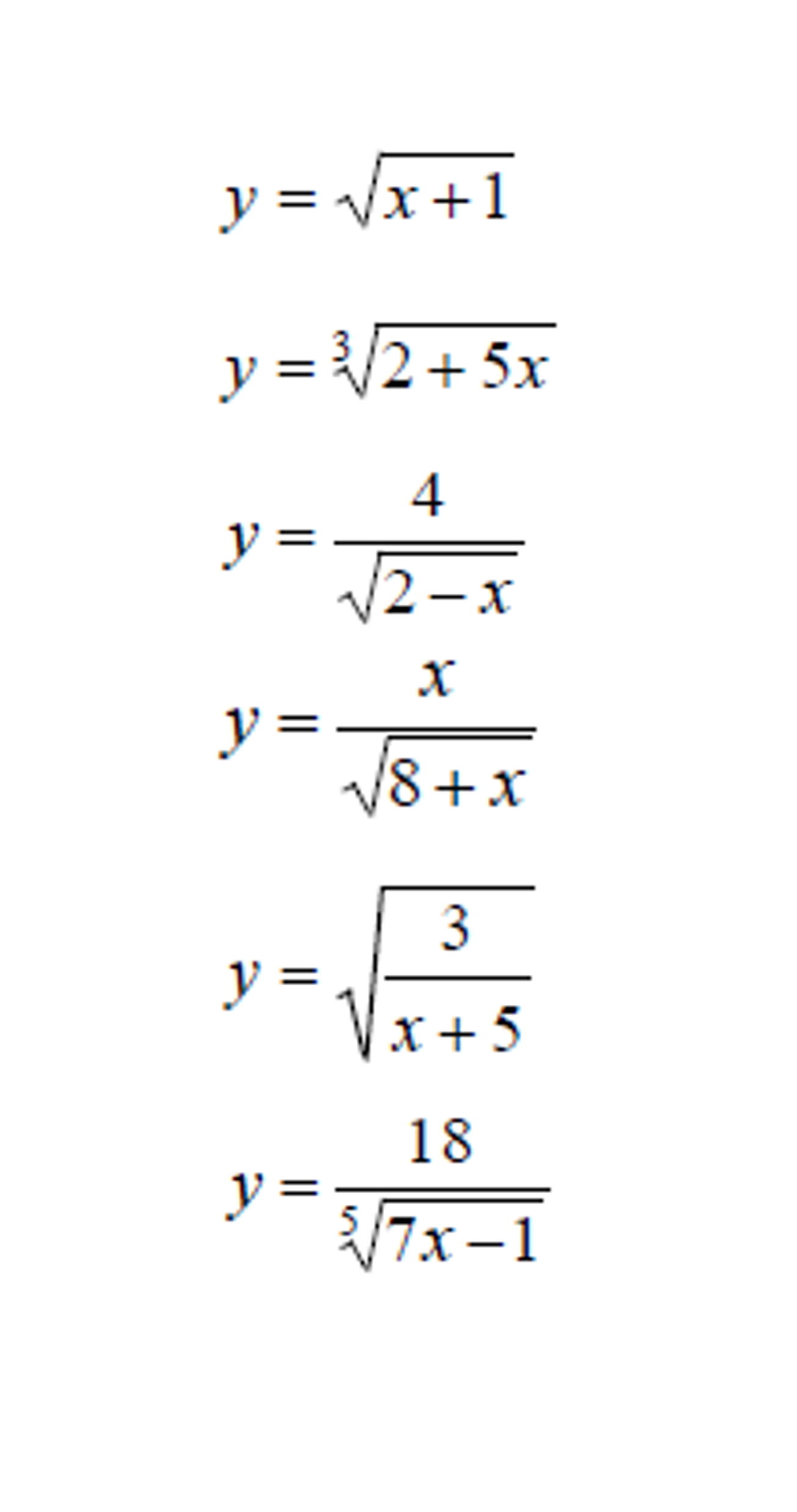
Indicaciones: Realiza un reporte PDF en donde incluyas la siguiente información siguiendo los criterios de la rúbrica de evaluación:

• Portada
• Introducción (mínimo media cuartilla)
• Desarrollo
  • Explica los pasos para encontrar los máximos y mínimos
  • Menciona qué es una función creciente y decreciente
  • Explica a través de imágenes, cuándo una función es cóncava hacia abajo y hacia arriba
  • Explica qué es el punto de inflexión
  • Explica cómo obtener un punto máximo y mínimo de la función: f(x) = x^3 - 3x^2 - 9x +1
  • Toma uno de los tres problemas de optimización aplicada a las derivadas y desarrollalo paso a paso
• Conclusiones (mínimo media cuartilla)
• Referencias (mínimo cinco no wikipedia, no buenas tareas, ni rincón del vago, ni nada por el estilo)